大学への数学Ⅲ&Cの勉強
以下の3次方程式の1つの根がわかっているときに
残りの2つの根を計算する問題があります。
この問題を自分で解く計算を間違えないために、その計算の答えを覚えておいて、その答えと照合して検算できるようになりましょう。
以下に、その答えを整理して書きましたので覚えてください。
【問題】
y=x3-ax と、 y=h との1つの交点のX座標の値がγである場合、他の交点のX座標の値αとβを求めよ。
この解の式は、yの微分(y’)を使ってあらわせます。
この解を求める計算には微分の計算はしていませんでしたが、2根の中点のyの微分が0になる場合は、その中点で重根を持つ(3次曲線がx軸に平行な直線と接する)関係をあらわすという意味を持っています。
この式は、そういう美しい数学の関係をあらわしていて興味深いです。
(こういう美しい数学の関係ばかりを入学試験に出す大学もあるようです。そういう大学の入学試験対策は、数学の美しい部分を探して覚える勉強が有効だと思います。)
以下に、正式に計算します。この計算結果を検算するために上の式を利用してください。
3乗の項にcが掛かっている3次方程式の答えは以下のようになります。
次に、以下の3次方程式の、1つの根がわかっている場合の残りの根を計算します。
以下に、正式に計算します。この計算結果を検算するために上の式を利用してください。

3乗の項にcが掛かっている3次方程式の答えは以下のようになります。
一般的な3次方程式の解は以下の式であらわせます。
以下で、微分の計算により、解に微分の式が用いられることを証明します。
以下では、c=1の場合を計算します。
(証明おわり)
(解の続き)
以上の計算の結果、平方根の式を使って、γ以外の2根を与える式が以下の式で得られた。
しかし、これで解答は終わらず、この式から根号を外すことができる。
根号を外す方法を以下の式の場合を例にして示す。
この式3の根の1つをγとする。
それ以外の根のαとβは以下の計算で得られていた。
この式の平方根の式は以下の式である。
この根号は、
「平方根の式を多項式に変換する問題」
のページの計算をすることで外すことができる。
その結論は、以下の式であらわされる。
(解答おわり)
【別解】
上の解以外に、3次方程式の1つの根を用いて他の根をあらわすることができます。
以下の式1の根の1つがαである場合、そのαを使って、他の根を以下ようにあらわせました。
ここで、αを以下の式4のkに置き換えてあらわす。
なぜこの式のkに置き換えるかという根拠は、全くの偶然で、そうすれば良いことが分かったからです。
この式6は、kを以下の式sに置き換えると、式1と同じ式8になります。そのためsは式1の根の1つ(それをβとする)をあらわします。
これで2つの根が求められたので、残りの根γは、式1の根と係数の関係を使って、以下の式で計算できます。
このように1つの根αが分かれば、式1の他の根が式10と式12で計算できました。
(解答の続き)
以上で求めた式β,γは、以上の分数式10,12に限らず、式3を使うことで、普通の多項式に変換できます。
(γの分数式の変換)
(βの分数式の変換)
結果を整理し以下の解が得られた。
(解答おわり)
リンク:
高校数学の目次
以下の3次方程式の1つの根がわかっているときに
残りの2つの根を計算する問題があります。
この問題を自分で解く計算を間違えないために、その計算の答えを覚えておいて、その答えと照合して検算できるようになりましょう。
以下に、その答えを整理して書きましたので覚えてください。
【問題】
y=x3-ax と、 y=h との1つの交点のX座標の値がγである場合、他の交点のX座標の値αとβを求めよ。
この解を求める計算には微分の計算はしていませんでしたが、2根の中点のyの微分が0になる場合は、その中点で重根を持つ(3次曲線がx軸に平行な直線と接する)関係をあらわすという意味を持っています。
この式は、そういう美しい数学の関係をあらわしていて興味深いです。
(こういう美しい数学の関係ばかりを入学試験に出す大学もあるようです。そういう大学の入学試験対策は、数学の美しい部分を探して覚える勉強が有効だと思います。)
以下に、正式に計算します。この計算結果を検算するために上の式を利用してください。
3乗の項にcが掛かっている3次方程式の答えは以下のようになります。
次に、以下の3次方程式の、1つの根がわかっている場合の残りの根を計算します。

3乗の項にcが掛かっている3次方程式の答えは以下のようになります。
以下では、c=1の場合を計算します。
(解の続き)
以上の計算の結果、平方根の式を使って、γ以外の2根を与える式が以下の式で得られた。
しかし、これで解答は終わらず、この式から根号を外すことができる。
根号を外す方法を以下の式の場合を例にして示す。
この式3の根の1つをγとする。
それ以外の根のαとβは以下の計算で得られていた。
この式の平方根の式は以下の式である。
この根号は、
「平方根の式を多項式に変換する問題」
のページの計算をすることで外すことができる。
その結論は、以下の式であらわされる。
(解答おわり)
【別解】
上の解以外に、3次方程式の1つの根を用いて他の根をあらわすることができます。
以下の式1の根の1つがαである場合、そのαを使って、他の根を以下ようにあらわせました。
ここで、αを以下の式4のkに置き換えてあらわす。
なぜこの式のkに置き換えるかという根拠は、全くの偶然で、そうすれば良いことが分かったからです。
この式6は、kを以下の式sに置き換えると、式1と同じ式8になります。そのためsは式1の根の1つ(それをβとする)をあらわします。
(解答の続き)
以上で求めた式β,γは、以上の分数式10,12に限らず、式3を使うことで、普通の多項式に変換できます。
(γの分数式の変換)
(βの分数式の変換)
結果を整理し以下の解が得られた。
(解答おわり)
リンク:
高校数学の目次



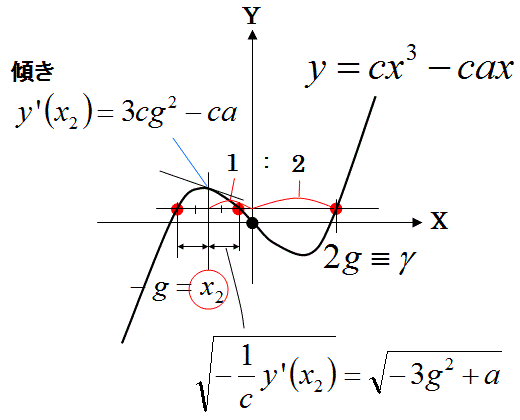



















0 件のコメント:
コメントを投稿