大学への数学Ⅲ&Cの勉強
行列と連立1次方程式
行列と連立1次方程式
以下のように、対角行列と回転行列の積の行列と、積が交換された、回転行列と対角行列の積の行列が等しいという条件が与えられているとする。
この式を計算すると以下の式になる。
この場合に、これらの行列の要素が以下の様に特定の値に制限される。この関係を、仮に、
「対角行列と回転行列の積の交換の定理」
と名づける。
行列の問題を解く際に、この定理の条件を与える式が得られたら、その式の解は、以下のように解けることを覚えておくと便利だと思う。
あるいは、この形の問題は以下の様に多くの解(選択肢)を持つという知識だけでも有用と思う。
上の行列の方程式から、以下の関係が得られる。
この問題では、以上のように、13個の場合分けされた解が得られる。
(補足)
この解のうちで、解1-1は、α=θであって、
(回転行列θ)(単位行列Eの定数倍)=(単位行列Eの定数倍)(回転行列θ)
の形をしています。
実は、 回転行列と積が交換される行列Aについては、すなわち、
(回転行列θ)(行列A)=(行列A)(回転行列θ)
を満足する行列Aは、
(単位行列を含む)回転行列(の定数倍)だけです。
後に学ぶことですが、積が交換可能な行列は、「固有ベクトル」を共有する行列のみであり、回転行列は共通する固有ベクトルを持つからです。
リンク:
追加講:三角形の面積と行列式
高校数学の目次



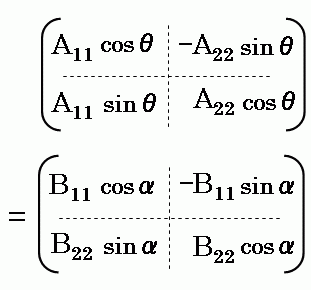








0 件のコメント:
コメントを投稿