大学への数学Ⅲ＆Ｃの勉強
行列と連立１次方程式
【解説】
上図のように、回転した楕円の位置座標（Ｘ，Ｙ）を行列Ａｋｓにより（Ｘ’，Ｙ’）に一次変換して楕円を円に変形する問題の続きを考える。
【総合解答の復習】
先の計算を復習する。
全ての Ａｔｍの解は以下のように計算できた。
ｂＸ２＋２ｄＸＹ＋ｃＹ２＝１ （１）
以下の形のＸ、Ｙに関する恒等式を組み立てる。
ｂＸ２＋２ｄＸＹ＋ｃＹ２＝（ｆＸ＋ｇＹ）２＋（ｈＸ＋ｋＹ）２ （２）
Ｘ’＝ｆＸ＋ｇＹ
Ｙ’＝ｈＸ＋ｋＹ
上の恒等式２を組み立てると、最初の式１は以下の式３に書き換えることができる。
Ｘ’２＋Ｙ’２＝１ （３）
以下では、先の式２が恒等式になるために必要なｆ，ｇ，ｈ，ｋの条件を求める。
ｆ２＋ｈ２＝ｂ （４）
ｇ２＋ｋ２＝ｃ （５）
２ｆｇ＋２ｈｋ＝２ｄ （６）
必要な条件は以上の式４から６である。
式４から式６の連立方程式を解く。
ｆ＝（√ｂ）ｃｏｓα （７）
ｈ＝（√ｂ）ｓｉｎα （８）
ｇ＝（√ｃ）ｓｉｎβ （９）
ｋ＝（√ｃ）ｃｏｓβ （１０）
上のように式７から式１０でｆ，ｇ，ｈ，ｋを定めると、式４と式５が成り立つ。
式６に式７から式１０を代入し、２で割ると以下の式を得る。
（√（ｂｃ））｛ｃｏｓα・ｓｉｎβ＋ｓｉｎα・ｃｏｓβ｝＝ｄ
ｓｉｎ（α＋β）＝ｄ／（√（ｂｃ）） （１１）
ここで、
α＋β＝θ （１２）
とおいて、式１１を書き換えると、
ｓｉｎ（θ）＝ｄ／（√（ｂｃ）） （１３）
この式１３により、θが定まる。
任意のαと、固定した値のθとで、ｆ，ｇ，ｈ，ｋ全てがあらわされる。
式７から式１０は以下の行列の式であらわされる。
【回転した楕円の軸ベクトルを計算する】
このように、楕円を描くベクトルを変換行列で円に変換できることがわかった。その変換行列のうち、以下のような特別な変換行列を求めて、それにより楕円の軸ベクトルを計算する問題を考える。
楕円を円に変換する変換行列の逆行列は、円を楕円に変換する。その円を楕円に変換する変換が、円を描くベクトルを、Ｘ軸方向とＹ軸方向で縮尺を変えて拡大・縮小して楕円を描かせ、そのベクトルを角度γで回転させる変換であるものとする。
そうして描かれた楕円をその操作を逆にして元の円に戻す変換の行列を計算する。
式７から式１３で定められる、楕円を円に変換する行列のうち、そのような条件を満足する変換の行列を計算する問題です。
（基本的解析方法）
この変換の逆変換によりを楕円に変換する式を計算して、その回転角度γに由来して楕円をあらわす方程式を計算して、その方程式の形とその楕円の回転角度との関係を計算する、のが一番良い解決方法と考える。
（別解その１）
その基本的解析方法は既に解説した。そのため、ここでは、その基本的解析結果の楕円の式からの情報を得ずに、楕円の式を円に変換する式を計算するのみの操作によって、そのように回転した楕円の軸のベクトルを計算することを考える。
その別解は、楕円の式から固有ベクトルを計算することが、良い解析方法と考える。
（別解その２）
固有ベクトルを計算する方法も既に解説したので、ここでは、固有ベクトルという便利な概念を使わずに、 楕円の式を円に変換する式を計算するのみの操作によって、そのように回転した楕円の軸のベクトルを計算する。
すなわち、楕円を円に変換する変換を逆にして、円を楕円に変換する変換が：
（１）円を描くベクトルを、Ｘ軸方向とＹ軸方向で縮尺を変えて拡大・縮小して楕円を描かせる。
（２）そのベクトルを角度γで回転させる変換。
という変換である特別な変換をあらわす行列を計算する。
しかし、正しく方程式を設定しても、それで問題を解き始めたら、解き方が難しい問題になった。
そのため、以下では、この問題を解き易くする計算技術を解説します。
【問題の条件の変換をあらわす方程式を求める】
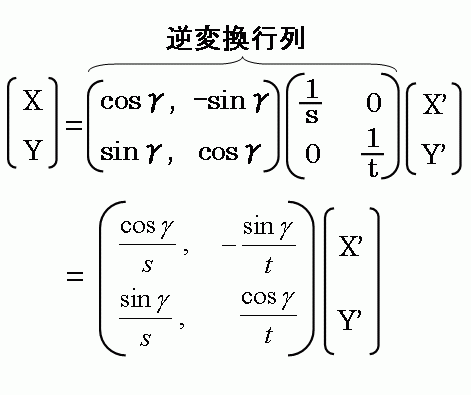
その逆行列Ａ－１が、
（１）円を描くベクトルを、Ｘ軸方向とＹ軸方向で縮尺を変えて拡大・縮小して楕円を描かせる。
（２）そのベクトルを角度γで回転させる。
という変換であるための条件は以下のように計算できる。
一方、先の計算の結果、 楕円を円に変換する行列の満たすべき条件が、式７から式１３で得られている。
それらは以下の式であらわされる。
この式に、逆行列Ａ－１の列ベクトル同士が直交して、内積が０になる条件を加えることで、問題を解くための連立方程式が完備し、以下の式になった。
しかし、これらの方程式を連立して解く問題は難しそうに思う。
そのため、少し遠回りになるかもしれないが、
そのため、少し遠回りになるかもしれないが、
未知数γとｓとｔを追加して、問題を以下のようにあらわす。
ここで、 γは、楕円の軸の回転角度をあらわす、問題が求める目的のパラメータを直接にあらわすものである。
なお、以上の式でパラメータｋ，ｈ，ｇ，ｆは、式を区別する記号として利用することにし、その値を計算する未知数としては扱わないことにする。
なお、以上の式でパラメータｋ，ｈ，ｇ，ｆは、式を区別する記号として利用することにし、その値を計算する未知数としては扱わないことにする。
以上の４つの式であらわすことで、ベクトルの内積が０になる条件式は既に組み込まれている。
そのため、問題が、上の４つの式に、ｓｉｎθが定数になる式を加えた連立方程式を解く問題に変わった。すなわち、問題が、未知数γとｓとｔを求める問題に変換された。
これらの未知数の間の関係を以下のように計算する。
以上によりパラメータｔとｓが求められた。
蛇足だが、もう少しｓとｔを調べる。
式１４と式１５から、
この結果を用いて変換行列Ａをあらわすと、以下のようになる。
（ｓとｔについては、表示を見易くするために、その計算結果は代入しないで、そのままｓとｔであらわす）
この変換行列の逆行列（それに比例する余因子行列）は以下のように計算できる。
その列ベクトルが求める楕円の軸ベクトルをあらわす。
以上の通り、楕円の軸ベクトルを計算できた。
（計算の反省）
以上のようにして楕円の軸ベクトルを計算できた。
しかし、その計算には煩雑な計算を必要とした。
楕円の軸ベクトルを計算する方法は、やはり、固有ベクトルを計算する方法が、より簡単に計算できる優れた方法であると考える。
【別解その２の別解】
総合解答の結果を利用せずに、以下のように直接に計算することもできる。
すなわち、変換行列Ａに関する式
を元にして、以下のように計算を行なう。
以上で、変換行列を定めるパラメータｓとｔとγが求められた。
この計算の形は、固有値を求めて固有ベクトルを求める計算のパターンと良く似ていると思う。
この計算の形は、固有値を求めて固有ベクトルを求める計算のパターンと良く似ていると思う。
リンク：
追加講：三角形の面積と行列式
高校数学の目次
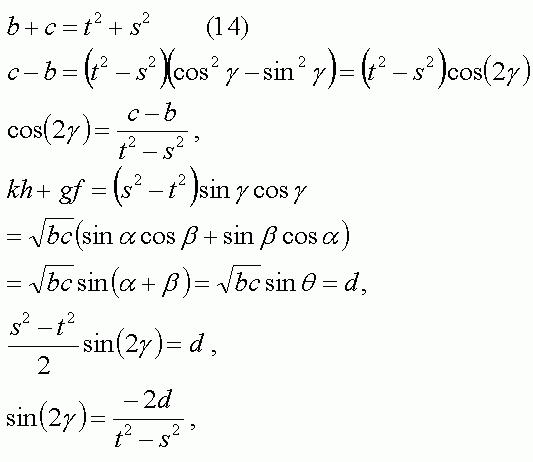
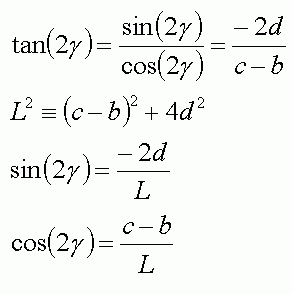
0 件のコメント:
コメントを投稿