積分の応用
【解説】
ループ状の曲線で全周囲を囲まれた図形の面積を計算するときには、以下のようにして計算すると計算ミスも少なく答えが得られますので覚えておきましょう。
上図のようなおむすび形の境界線の（ｘ，ｙ）座標がパラメータθの関数であらわされていて、パラメータθを増すと、（ｘ，ｙ）点が領域の境界線を一周するものとします。
この場合に、上図の図形のｘ方向の幅が細い微小面積であってその先端が図形の境界位置でｙ座標が大きい側にある微小面積を考え、それをｘ方向の正方向に積分することで面積を加算します。
次に、上のような、図形のｙ座標が小さい側の境界を先端にするｘ方向の幅が細い微小面積をｘ方向の負の方向に積分することで、負の面積を加算します。すなわち、ｙ座標が小さい側の境界を先端にする、余分に加算された面積を引き算します。
これにより全面積の加減算を行うことで、求める面積は、上の式であらわされるように、パラメータθを用いた１つの単純な積分計算に帰着します。
上のような、図形のｘ座標が大きい側の境界を先端にすろｙ方向の幅が細い微小面積をｙ方向の負方向に積分した値にマイナス１を掛け算することで面積を加算します。
次に、上のような、図形のｘ座標が小さい側の境界を先端にするｙ方向の幅が細い微小面積をｙ方向の正の方向に積分した値にマイナス１を掛け算することで、負の面積を加算します。すなわち、ｘ座標が小さい側の境界を先端にする、余分に加算された面積を引き算します。
これにより全面積の加減算を行うことで、求める面積は、パラメータθを用いて、上の式であらわされるように、１つの単純な積分計算に帰着します。
上図のような曲線の境界線の（ｘ，ｙ）座標がパラメータθの関数であらわされていて、パラメータθを増すと、（ｘ，ｙ）点が領域の境界線を１方向に移動するものとします。
この場合に、その曲線とｘ軸とで周囲を囲まれた図形の面積を計算するには、以下のように計算します。
先ず、上のような、図形のｙ座標が大きい側の境界を先端にする微小面積をｘ方向の正方向に積分することで面積を加算します。
次に、上のような、図形のｙ座標が小さい側の境界を先端にするｘ方向の幅が細い微小面積をｘ方向の負の方向に積分することで、負の面積を加算します。すなわち、ｙ座標が小さい側の境界を先端にする、余分に加算された面積を引き算します。
これにより全面積の加減算を行うことで、求める面積は、パラメータθを用いて、上の式であらわされるように、１つの単純な積分計算に帰着します。
上図のようなｙ座標が負である曲線の境界線とｘ軸とで周囲を囲まれた図形の面積を計算するには、上の式で計算します。
求める面積は、パラメータθを用いて、上の式であらわされるように、１つの単純な積分計算に帰着します。
【問題】
以下の式のように、 境界線の（ｘ，ｙ）座標がパラメータθの関数であらわされていて、パラメータθを増すと、（ｘ，ｙ）点が領域の境界線を一周する場合に、このループ状の曲線で全周囲を囲まれた図形の面積Ｓを計算せよ。
（問題おわり）
この問題は、上で説明したようにパラメータθで単純な積分計算をすることで解けます。
試験問題で上の積分計算を利用して解答を書く場合は、（時間に余裕があったら）上の説明を簡単に解答に書いて、その計算の正当性を説明するようにしてください。
（解答はじめ）
（解答おわり）
リンク：
高校数学の目次
【解説】
ループ状の曲線で全周囲を囲まれた図形の面積を計算するときには、以下のようにして計算すると計算ミスも少なく答えが得られますので覚えておきましょう。
この場合に、上図の図形のｘ方向の幅が細い微小面積であってその先端が図形の境界位置でｙ座標が大きい側にある微小面積を考え、それをｘ方向の正方向に積分することで面積を加算します。
この場合に、その曲線とｘ軸とで周囲を囲まれた図形の面積を計算するには、以下のように計算します。
先ず、上のような、図形のｙ座標が大きい側の境界を先端にする微小面積をｘ方向の正方向に積分することで面積を加算します。
求める面積は、パラメータθを用いて、上の式であらわされるように、１つの単純な積分計算に帰着します。
【問題】
以下の式のように、 境界線の（ｘ，ｙ）座標がパラメータθの関数であらわされていて、パラメータθを増すと、（ｘ，ｙ）点が領域の境界線を一周する場合に、このループ状の曲線で全周囲を囲まれた図形の面積Ｓを計算せよ。
この問題は、上で説明したようにパラメータθで単純な積分計算をすることで解けます。
試験問題で上の積分計算を利用して解答を書く場合は、（時間に余裕があったら）上の説明を簡単に解答に書いて、その計算の正当性を説明するようにしてください。
（解答はじめ）
リンク：
高校数学の目次
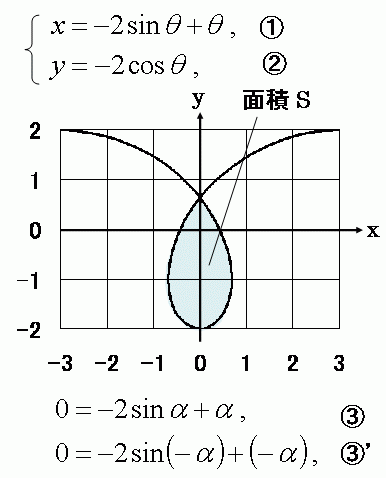
0 件のコメント:
コメントを投稿