3乗すると単位行列になる行列が使われる場合がありますので、以下で、3乗すると単位行列になる行列を求めてみます。
その行列を、以下の行列要素の性質を利用して求めます。
3乗すると単位行列になる行列Mを、これらの行列要素の和に分解して考えます。
(注意)以下の計算で、gのパラメータが複素数になる解もあります。その解も正しい解ですが、とりあえず、係数gが実数の場合の行列だけを求めることにします。
また、Hが0行列であってMがもともと単位行列であったという自明な解を省きます。
この式①と②が求める行列の条件をあらわしています。
この条件を満足する行列は無限に多くあります。
以下では、その中のいくつかをピックアップして、いくつかの具体的な行列を計算します。
リンク:
高校数学の目次

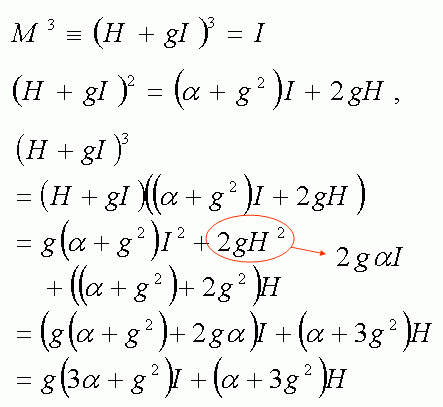



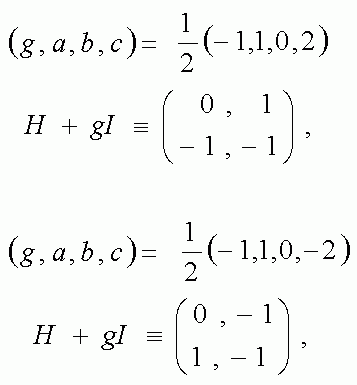



0 件のコメント:
コメントを投稿