

大学への数学Ⅲ&Cの勉強
行列と連立1次方程式
【解説】
対角行列Bmkから、以下の様にして行列式Δが0では無い行列Psmを使って、固有値が同じ行列Astを作ることができます。
行列Ast固有値λは以下の行列式により得られます。
対角行列からでは無くても、同様に変換された行列同士の固有値λは等しくなります。
この行列Astの意味を以下で説明します。
あるベクトルXkと、そのベクトルが対角行列Bmkにより変換された結果のベクトルYmとがある場合:
Ym=BmkXk (1)
その2つのベクトルを、行列Psmで新しいベクトルX’sとY’sに変換した場合に、その新しいベクトル間の変換の行列をAstであらわせるものとします。
X’s=PsmXm (2)
PsmYm=AstPtkXk,
P-1usを左から掛け算する。
P-1usPsmYm=P-1usAstPtkXk,
Yu=P-1usAstPtkXk,
(1)を代入する。
BukXk=P-1usAstPtkXk,
上式が任意のベクトルXkで成り立つ条件を求める。
それは、ベクトルXkの各成分毎に、係数同士が等しいことである。
それは、以下の式になる。
Buk=P-1usAstPtk
Pwuを左から掛け算し、P-1kmを右から掛け算する。
PwuBukP-1km=PwuP-1usAstPtkP-1km=EwsAstEtm
PwuBukP-1km=Awm
ベクトル(1,0)が行列Bukで変換されてベクトルλ1(1,0)になる。
その各ベクトルをPsmで1次変換すると、
変換されたベクトル同士では、縦ベクトルPt1が行列Astによって縦ベクトルλ1Pt1に変換される関係になる。
すなわち、行列Astに関しては、縦ベクトルPt1が固有値λ1についての固有ベクトルです。
そのため、Ptkは固有ベクトルを並べた行列になっている。
つまり、以下の式が成り立ちます。
ここで、
PwuBukP-1km=Awm
という式や、
Buk=P-1usAstPtk
という式は、以下のように覚え易い形に変形して覚えます。
PsuBukXk=AstPtkXk
右辺は、ベクトルXkを前もってPtkで1次変換してしておいて、1次変換後のベクトルを行列Astで変換する操作です。
左辺の操作は右辺の操作と同じ結果を出します。
特に、左辺では、対角行列Bukによって、ベクトル(1,0)を第1の固有値倍に変換し、ベクトル(0,1)を第2の固有値倍に変換します。
右辺では、それらのベクトルがPtkで1次変換された結果のベクトル、すなわち、行列Ptkの縦ベクトルが固有値倍に変換されます。
以上の結果から、 行列Astの固有値を計算して、その固有値に対応する2つの固有ベクトルを計算して、その2つの固有ベクトルを並べた行列Ptkを使えば、行列Astを行列Ptkによって対角化した行列Bmkを逆算することができます。
行列Astから対角化した行列Bmkを求めることを、行列の対角化と言います。
(固有値が同じ行列の例)
行列AwuBukと行列BwuAukとは等しくない場合が多いですが、
A-1km(AmuBus)=Bks=(BkmAmu)A-1us
が成り立ちます。
そのため、 行列AwuBukと行列BwuAukとは同じ固有値を持ち、行列A-1kmによって互いに変換されます。
また 、行列AwuBukと行列BwuAukは同じ固有値を持つので、固有値の和をあらわす行列の対角成分の和も同じになります。
つまり、
tr(AB)=tr(BA)
です。
(固有値が同じ行列の性質)
そういう行列Aでも、固有値を求める上記のn行n列の行列式の、
x(n-1)の係数=-固有値の和=-行列Aの対角要素の和
になります。
そのため、いずれにしろ、
固有値の和=行列Aの対角要素の和
が成り立ちます。
(注意)
固有値が同じ行列同士を変換する行列Ptkが求められるためには、変換される行列Astの固有ベクトルが2つなければなりません。
大学生も間違え易い問題点ですが、
行列Astの固有ベクトルが2つあるのは、以下の場合のみです。
(1)その2つの固有値が異なる場合。
(2)その2つの固有値αが等しいが、行列Ast=α・Estである場合。
2つの固有値が等しい場合で、行列Astが単位行列の固有値倍の行列では無い場合は、固有ベクトルは1つしかありません。その行列Astは、どの行列Ptkで変換しても、対角化された行列には変換できません。
(第2の方法)
次に、行列Ptkで変換しない方法で、固有値が同じ行列を作る方法を説明します。
固有値が同じ行列では対角要素の和(すなわち、固有値の和)が変わらないので、以下のような行列の足し算を考えます。
ここで、行列Astの固有値は以下の式で計算できます。
この式を満足するパラメータaを持つ行列を足し合わせると、その行列の固有値は変わりません。
この変換方法では、2つの固有値が等しい場合で、行列Astが単位行列の固有値倍の行列では無い場合にも、その行列Astから対角化された(固有値が等しい)行列を作ることができます。
しかし、この変換は、単に固有値が同じ行列を作るだけの処理です。
行列Ptkで1次変換して行列を作るわけではないので、作られた行列の性質が元の行列の性質と同じであるという保証はありません。
【固有値が重根の場合の、固有値が等しい行列】
以下では、固有値が重根の場合に、固有値が同じ行列を作ってみます。
単位行列の定数倍の対角行列から、1次変換によって固有値が等しい行列を作ると、その結果は元の行列と変わりません。
そのため、固有値が重根であって対角行列で無い行列は、どのように1次変換しても決して対角行列にはならないのです。
《重根の固有値を持つ第1の例》
次に、先に説明した第2の方法で、単位行列と固有値が等しい(固有値が1の重根を持つ)行列を作ってみます。
この新しい行列は元の行列と同じで固有値1を持ちます。この新しい行列の固有ベクトルは(1,1)に比例するベクトルだけです。
それ以外のベクトル(F1, F2)は、
F1(2,1)+F2(-1,0)
=F1((1,0)+(1,1))+F2((0,1)+(-1,-1))
=(F1,F2)+(F1-F2)(1,1)
に変換します。
変換の結果の方向が変わらないベクトル、すなわち、固有値倍に変換されるベクトルはベクトル(1,1)の方向のベクトルのみです。
そもそも固有値は、固有ベクトルを求める式が源になって定義されたパラメータです。
この場合は、その求める対象の固有ベクトルが1つしか無いので、
固有値が重根(重解)となって2つ得られたというのは見せかけであって、1つの固有値しか得られていないと解釈できます。
《重根の固有値を持つ第2の例》
また、固有値が1の重根を持つもう1つの行列A:

は、固有ベクトル

を1つのみ持つ。


リンク:
固有ベクトルを求める(裏技)
追加講:三角形の面積と行列式
高校数学の目次



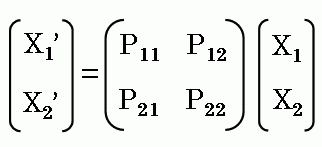
















0 件のコメント:
コメントを投稿