

大学への数学Ⅲ&Cの勉強
行列と連立1次方程式
以下の説明は少し長くなります。回転した楕円の式を手っ取り早く求める方法を次ページに書きましたので、楕円の式のみに興味のある人は次のページに進んでください。
(ただし、このページの最後の、楕円の軸ベクトルの公式は見て欲しい。)
【解説】
直線を座標原点を中心に回転させる場合は、以下の図のように、回転した直線の方程式が求められます。

直線の式は、直線上の点の位置ベクトルと単位ベクトル
の内積が直線と原点との間の距離cであるという関係をあらわす式ですので、
直線を回転すると、その単位ベクトル
が回転します。
それで、回転した直線の式は単位ベクトル
を回転変換することで求められます。
座標(X,Y)を(X’,Y’)に変換する、回転変換の行列を
とします。
また、その逆回りの(-θの)回転変換の行列は、
です。
次に、楕円を座標原点を中心に回転させる場合を、
以下の図で考える。

楕円の式は、楕円の軸をXY座標軸に合わせるように回転を巻き戻した場合の式はわかっています。そのため、回転した楕円上の点(X,Y)を、回転を巻き戻した楕円上の点(X’,Y’)に変換して、その点のXY座標を楕円の式であらわします。
回転した楕円上の点の座標(X,Y)を(X’,Y’)に変換する、回転の巻き戻し変換の行列は、直線の回転の場合と同じ、
です。
以下では、この行列による座標の変換の式を楕円の式に代入して、その代入した式を変形することで回転した楕円の式を計算します。
すなわち、
以上の計算結果をまとめると、
こうして、回転した楕円をあらわす方程式が計算できました。
回転した楕円の方程式をあらわすために対称行列
を利用しました。
この楕円をあらわす方程式の左辺
は、
との内積を計算する式です。
すなわち、べクトル
を行列
で変換して作ったベクトル
と元のベクトル
との内積を計算する式です。
元のベクトル
が固有ベクトルのとき、
固有ベクトルは、
行列
で変換されると、
(行列の固有値λ)倍に拡大されます。
その様に拡大された固有ベクトルと、元の固有ベクトルとの内積の計算結果は、
(元の固有ベクトルの長さの2乗)×(行列の固有値λ)
になります。
一方で、元のベクトル
が固有ベクトルでは無い場合は、
を回転変換することで求められます。
座標(X,Y)を(X’,Y’)に変換する、回転変換の行列を
とします。
また、その逆回りの(-θの)回転変換の行列は、
です。
次に、楕円を座標原点を中心に回転させる場合を、
以下の図で考える。

楕円の式は、楕円の軸をXY座標軸に合わせるように回転を巻き戻した場合の式はわかっています。そのため、回転した楕円上の点(X,Y)を、回転を巻き戻した楕円上の点(X’,Y’)に変換して、その点のXY座標を楕円の式であらわします。
回転した楕円上の点の座標(X,Y)を(X’,Y’)に変換する、回転の巻き戻し変換の行列は、直線の回転の場合と同じ、
です。
以下では、この行列による座標の変換の式を楕円の式に代入して、その代入した式を変形することで回転した楕円の式を計算します。
すなわち、
以上の計算結果をまとめると、
こうして、回転した楕円をあらわす方程式が計算できました。
回転した楕円の方程式をあらわすために対称行列
を利用しました。
この楕円をあらわす方程式の左辺
は、
ベクトル
とべクトルとの内積を計算する式です。
すなわち、べクトル
を行列
で変換して作ったベクトル
と元のベクトル
との内積を計算する式です。
元のベクトル
が固有ベクトルのとき、
固有ベクトルは、
行列
で変換されると、
(行列の固有値λ)倍に拡大されます。
その様に拡大された固有ベクトルと、元の固有ベクトルとの内積の計算結果は、
(元の固有ベクトルの長さの2乗)×(行列の固有値λ)
になります。
一方で、元のベクトル
が固有ベクトルでは無い場合は、
2行2列行列Fで変換されたベクトルは、元のベクトルとは平行ではありません。
《楕円を表す対称行列Fの行列式》
回転する前の楕円の式は、対称行列Fの替りに、以下の対称行列Dを利用して表された式です。
この、楕円が回転する前の対称行列Dと、
楕円が回転した後の対称行列Fとでは、
以下の式であらわす行列式の値が同じになります(この証明は省略します。読者の各自で証明しておいてください)。
そのため、回転した楕円の方程式を表す対称行列Fについて、上式で表す行列式を計算することで、
回転する前の楕円を表す対称行列Dの行列式がわかります。
回転する前の図形が双曲線の場合は、その双曲線を表す対称行列Dの行列式の値が負になり、楕円の場合では値が正になる事と区別できます。
《楕円の回転角度の計算》
次に、回転した楕円の式が与えられたとき、その楕円はどれくらいの角度回転した楕円であるか、その回転角度を楕円の式から計算する方法を考えます。
その方法は、以下の楕円の軸の性質を利用します。


なお、この軸ベクトル
です。

なお、この軸ベクトル
です。
以上のように、回転した楕円の軸ベクトルは、
対称行列
の固有ベクトルです。そのため、
対称行列
の固有ベクトルを計算すれば回転した楕円の回転角度がわかります。
なお、回転した楕円の軸の長さaとbは、以下のように固有値λを計算して、固有値λの解の、
を得ることでわかります。
∴ 固有値λの解の、
が得られました。
楕円の方程式は、固有ベクトルの方向では、
ベクトルの長さの2乗×固有値=1
すなわち、
ベクトルの長さの2乗=1/固有値
よって、そのベクトルの長さはaとbです。
以下で、この固有値λ毎に固有ベクトルを計算します。

《1》
固有値λが
の場合:
行列
を計算する。
この行列は、固有ベクトルを0ベクトルに変換する、行列式が0である行列です。
行列式が0になる行列は、その余因子行列の縦ベクトルを0ベクトルに変換するので、
この固有値λを使って作ったこの行列の固有ベクトルは、その余因子行列の縦ベクトルに比例する。
そのため、この行列の余因子行列
を求める。
その行列Hは、以下の式になる。
この余因子行列Hの縦ベクトル
は、固有ベクトルに比例する。
詳しくは、以下の縦ベクトルである。
ここで、
の場合に、 このベクトルを
で割り算すると、
という固有ベクトルが得られる。
あるいは、
の場合に、
を
で割り算すると、
同じく、
が固有ベクトルとして得られる。結局、
の場合に、
が固有ベクトルとして得られる。この固有ベクトルは、楕円の軸ベクトル
である。
《2》
固有値λが
の場合:
行列
は、
a→b,b→a,cosθ→sinθ,sinθ→-cosθという置き換えをしたら同じ式になるので、
固有値
の固有ベクトルの解を、そのように置き換えることで、
固有値
の固有ベクトルの解になる。
∴ 固有ベクトルは、
これは、楕円の軸ベクトル
である。
(蛇足)
固有ベクトルを求めて楕円の回転角度を求める以外の方法で楕円の回転角度(-θ)を計算する方法として、以下のようにしても角度θを計算できる。
の場合に、
こうして、回転した楕円の式から、楕円の回転角度の2倍のタンジェントが計算できる。
この、楕円の回転角度2θの公式を導く方法として、固有ベクトルが同じ行列(対称変換行列)を計算することで、この公式を導くこともできる。
【楕円の軸ベクトル(固有ベクトル)の公式】
一方、以上の計算の結果の、対称行列Fの固有ベクトル(角度-θ方向の、楕円の軸の方向のベクトル)をあらわす公式は以下のようにあらわせる。上の蛇足の公式を覚えるよりは、以下の計算手順を含めた公式を覚える方が覚え易いのではないかとも考える。
以下の、回転した楕円をあらわす式が与えられた場合、
先ず、この式の元になっている対称行列Fの固有値λを以下の式で計算する。
この固有値λの各解毎に、以下のように固有値λに対応する固有ベクトルが計算できる。
ここで、固有ベクトルを表す上の式の右辺の第1項の単位ベクトルに比例する以下のベクトルを計算する。
そのベクトルを使い、固有ベクトルを表す式の右辺を以下の式の左辺に表します。
以下の式の左辺のベクトルを計算すると右辺のベクトルになります。

この式の右辺のベクトルの係数を除去すると、先に計算した楕円の軸ベクトルの計算結果に一致します。
先に説明した蛇足の公式は、上の式の左辺の第1項の単位ベクトルに比例するベクトルのx座標とy座標の比を計算するものです。


リンク:
追加講:三角形の面積と行列式
高校数学の目次
▷(参考)新型コロナウイルス感染対策



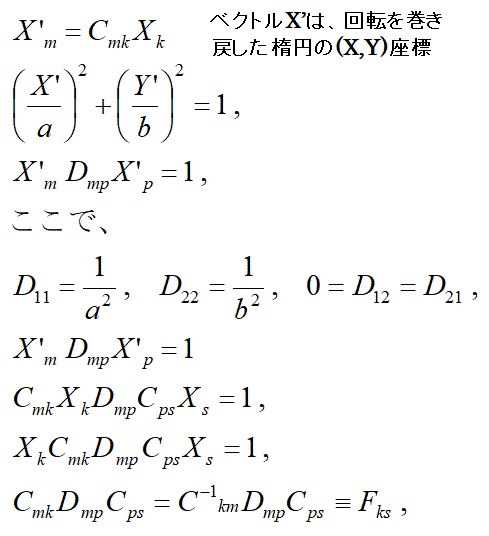











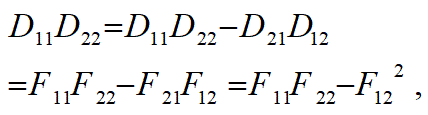










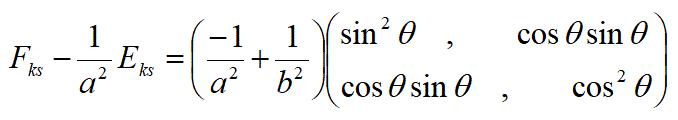


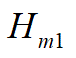













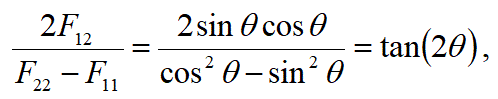




0 件のコメント:
コメントを投稿