

佐藤の数学教科書「図形と方程式」編の勉強
上図のように頂点の1つが原点Oにあり、他の2頂点が、A(a1,a2)とB(b1,b2)である三角形OABの面積を求めると以下の式になる。
△OAB=四角形OMPN-{△OMA+△OBN+△APB}
三角形の頂点Oを任意の座標位置にある頂点C(c1,c2)であるものとして、上の面積をあらわす公式を、3頂点A,B、Cの座標であらわすと、下の式になる。
「クロス積」は、正式な名前では、「行列式」と呼ばれています。
行列式は、その名前だけを高校3年の数学Cで学びます。
しかし、行列式が持つ以下の性質は、高校数学では教えないことになっているようです。
クロス積(行列式)は、Bの行にAの行の任意数(k)倍を足し算しても、値が変わらない。列も同様です。
(なお、クロス積は、行と列を入れ替えても値が変わりません)
例えば、下のようにBの行にAの行の(-1)倍を加えても、行列式の値は変わりません。
さらに、一番上の行のみ(-1)を掛け算すれば、値が(-1)倍になります。その行列式全体に(-1)を掛け算したものは最初の行列式と値が同じ以下の形になります。
クロス積(行列式)の形になった数式は「きれいな数式」です。
クロス積(行列式)の形の数式は、最も単純な形であらわせた数式と考えて良いです。
上の2つ前の(式2)の行列式に対して、一番上の行に、下の行を加えても、行列式の値は変わらず、以下の式になります。
結局、上の三角形の面積の公式のクロス積(行列式)の部分は、
(1)点Cを中心として計算したクロス積(行列式)
(2)点Aを中心として計算したクロス積(行列式)
(補足)この行列式全体に掛っている(-1)を無くすには、上の行と下の行を入れ替えて(-1)を取り除いた以下の行列式に置き換えてください。
(3)点Bを中心として計算したクロス式(行列式)
値が同じ3種類のクロス積(行列式)であらわせますが、
そのどれもが、最も単純な式と考えてください。
そのクロス積(行列式)を展開した別の式を求めても、その式は単純では無い式になり、単純な形のクロス積(行列式)の形の表示から退化した形の式に変わってしまいます。
複素数平面を使うと「3つの複素数の交代式の簡単化公式」、このクロス積を展開してもさほど複雑では無い対称式でクロス積の内容をあらわすことができます。


リンク:
三角形の面積をベクトルで分解して計算する
高校数学の目次
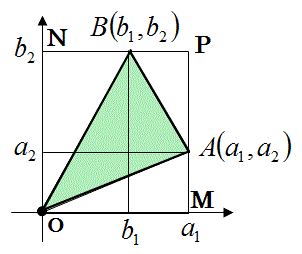











0 件のコメント:
コメントを投稿