【解説】
直線を座標原点を中心に回転させた場合の楕円の方程式を考える。
先ず、回転する前の楕円の方程式は以下の図のようにあらわせます。
この楕円を、以下の図のように、原点の回りに角度θ回転させます。
ここで、楕円の軸方向のベクトルｇとｈを考えます。
この軸ベクトルｇとｈを使って楕円上の点Ｐの位置ベクトルをあらわすことにすると、以下の式が成り立つ。
そして、楕円の式を変形して、楕円の式の意味を考える。
回転した楕円の方程式を、楕円上の点Ｐの位置ベクトルＰに対するべクトルの関数Ｆを使って、そのベクトルＦと位置ベクトルＰとの内積が１になる方程式であると解釈します。
そのベクトル関数Ｆは、以下の式のように、楕円の２つの軸方向の各ベクトルを、それぞれ異なる倍率１／ａ２と１／ｂ２倍のベクトルに拡大するベクトル関数であると解釈できます。
楕円をあらわすベクトル方程式のベクトル関数ＦがＸＹ座標方向の単位ベクトルｘとｙに対してはどのように作用するかを調べてみます。
上の式のように、単位ベクトルｘに関するベクトルＦと単位ベクトルｙとの内積は、単位べクトルｙに関するベクトルＦと単位ベクトルｘとの内積に等しい関係があります。
次に、下の図のように、ベクトルＰを、単位ベクトルｘのＸ倍のベクトルと、単位ベクトルｙのＹ倍のベクトルの和であらわします。
そのベクトルＰに関する楕円の方程式を以下のように計算します。
すなわち、回転した楕円の方程式を、位置ベクトルに対するべクトルの関数Ｆを使って、以下の式であらわした。
このように、系数Ａ，Ｂ，Ｃを使ったＸ座標とＹ座標の関数で楕円があらわされる。
【問１】
以下の方程式で表される図形が、回転した楕円であるか、回転した双曲線であるか、２本の直線であるかを判定する条件を求めよ。
直線を座標原点を中心に回転させた場合の楕円の方程式を考える。
先ず、回転する前の楕円の方程式は以下の図のようにあらわせます。
この軸ベクトルｇとｈを使って楕円上の点Ｐの位置ベクトルをあらわすことにすると、以下の式が成り立つ。
そして、楕円の式を変形して、楕円の式の意味を考える。
そのベクトル関数Ｆは、以下の式のように、楕円の２つの軸方向の各ベクトルを、それぞれ異なる倍率１／ａ２と１／ｂ２倍のベクトルに拡大するベクトル関数であると解釈できます。
上の式のように、単位ベクトルｘに関するベクトルＦと単位ベクトルｙとの内積は、単位べクトルｙに関するベクトルＦと単位ベクトルｘとの内積に等しい関係があります。
次に、下の図のように、ベクトルＰを、単位ベクトルｘのＸ倍のベクトルと、単位ベクトルｙのＹ倍のベクトルの和であらわします。
そのベクトルＰに関する楕円の方程式を以下のように計算します。
すなわち、回転した楕円の方程式を、位置ベクトルに対するべクトルの関数Ｆを使って、以下の式であらわした。
このように、系数Ａ，Ｂ，Ｃを使ったＸ座標とＹ座標の関数で楕円があらわされる。
【問１】
以下の方程式で表される図形が、回転した楕円であるか、回転した双曲線であるか、２本の直線であるかを判定する条件を求めよ。
この問題の解答はここをクリックした先のページに書きました。
【問２】
このような形で原点の回りに回転した楕円の方程式が与えられたとき、その楕円の回転軸の方向を計算する公式を求めよ。
この問題を解くために、ベクトル関数Ｆは、Ｘ座標の方向の単位ベクトルｘと、Ｙ座標の方向の単位ベクトルｙを、系数Ａ，Ｂ，Ｃを使った以下の式で新たなベクトルに変換する関数であると考える。
こうしてベクトル関数Ｆの形が定められた。
次に、このベクトル関数Ｆによってベクトルの方向が変えられないベクトルｇとｈを求める。
そのベクトルｇとｈが楕円の軸方向のベクトルであり、以下の図であらわすように、回転した楕円の軸方向のベクトルを表わしている。
できれば、この問題を自力で解いて欲しい。 その方が、楽しく数学を学べると思いますので。
この問題の解答はここをクリックした先のページに書きました。
リンク：
高校数学の目次
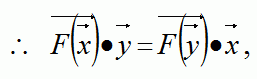
0 件のコメント:
コメントを投稿