「大学への数学ⅢC」の勉強
【研究問題】
座標原点を中心にする楕円
と、円A
とが接する接点Pにおける接線を、
接点Pから円Aの中心に向かう単位ベクトルC(xc,yc)に垂直な直線の式、
であらわされるものとした場合に、
(1)その接線と楕円の中心の距離mの値を求めよ。
(2)円Aの中心の座標A(x1,y1)の値をxc,yc,m,rであらわす式を求めよ。
(解答)
以下では、この問題を、単位ベクトルC(xc,yc)の値が先に分かっている場合から始めて解く。
楕円
に接する直線は、単位ベクトルC(xc,yc)に垂直な直線であり、接点:
での接線の式は、楕円の接線の公式により、
である。
この接線の式が式3と等しいとして、以下の式4を導く。
式4の座標値を式3に代入して以下の計算をすることで式5が得られる。
式5により、楕円の中心と直線との距離mをxcとycから計算することができる。
mの値は、正の値と負の値との2つです。
式3のmが、この式5で得られる。
円Aの中心の座標A(x1,y1)の値は以下の式であらわせる。
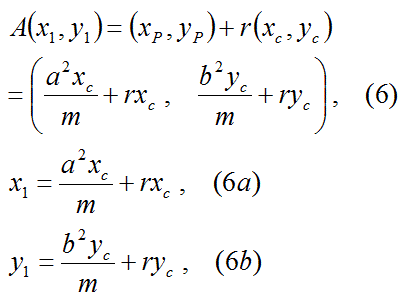
このように、最初に、楕円への接線に垂直な単位ベクトルC(xc,yc)がわかれば、他のパラメータが簡単に計算できる。
しかし、他のパラメータから、xc,ycを計算しようとすると簡単ではありません。
例えば、xcを他のパラメータから計算する式を、以下で求めてみます。
式6aを変形する。
mに式5を代入してmを消去する。
単位ベクトルCの成分の関係式
を用いて、ycをxcであらわす。
この式はxcに関する4次方程式である。
すなわち、xcを他のパラメータから計算しようとすると、4次方程式の解を求める問題に帰着する。
この4次方程式の解は簡単には解けない。その解を得るには、EXCEL等を利用して近似解を計算するしかない。
よって、xcを他のパラメータから計算する問題は入学試験などの試験には出題されない。
(たまたま簡単に解ける4次方程式になる場合だけが試験に出題され得るだろう。)
リンク:
高校数学の目次
【研究問題】
座標原点を中心にする楕円
と、円A
とが接する接点Pにおける接線を、
接点Pから円Aの中心に向かう単位ベクトルC(xc,yc)に垂直な直線の式、
(1)その接線と楕円の中心の距離mの値を求めよ。
(2)円Aの中心の座標A(x1,y1)の値をxc,yc,m,rであらわす式を求めよ。
(解答)
以下では、この問題を、単位ベクトルC(xc,yc)の値が先に分かっている場合から始めて解く。
楕円
に接する直線は、単位ベクトルC(xc,yc)に垂直な直線であり、接点:
での接線の式は、楕円の接線の公式により、
である。
この接線の式が式3と等しいとして、以下の式4を導く。
式4の座標値を式3に代入して以下の計算をすることで式5が得られる。
式5により、楕円の中心と直線との距離mをxcとycから計算することができる。
mの値は、正の値と負の値との2つです。
式3のmが、この式5で得られる。
円Aの中心の座標A(x1,y1)の値は以下の式であらわせる。
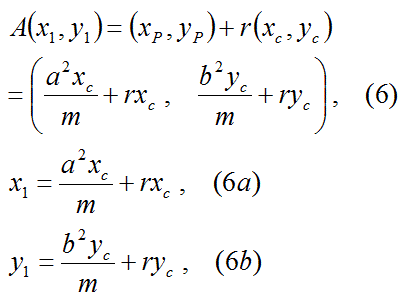
このように、最初に、楕円への接線に垂直な単位ベクトルC(xc,yc)がわかれば、他のパラメータが簡単に計算できる。
しかし、他のパラメータから、xc,ycを計算しようとすると簡単ではありません。
例えば、xcを他のパラメータから計算する式を、以下で求めてみます。
式6aを変形する。
単位ベクトルCの成分の関係式
を用いて、ycをxcであらわす。
この式はxcに関する4次方程式である。
すなわち、xcを他のパラメータから計算しようとすると、4次方程式の解を求める問題に帰着する。
この4次方程式の解は簡単には解けない。その解を得るには、EXCEL等を利用して近似解を計算するしかない。
よって、xcを他のパラメータから計算する問題は入学試験などの試験には出題されない。
(たまたま簡単に解ける4次方程式になる場合だけが試験に出題され得るだろう。)
リンク:
高校数学の目次












0 件のコメント:
コメントを投稿